改進此頁

Binary Tree - 二元樹

二元樹是每個節點最多有兩個子樹的樹結構，子樹有左右之分，二元樹常被用於實現二元搜尋樹(binary search tree)和二元堆(binary heap)。

二元樹的第i層(根結點為第1層，往下遞增)至多有 $2^{i-1}$ 個結點；深度為k的二元樹至多有 $2^k-1$ 個結點；對任何一棵二元樹T，如果其終端結點數為 $n_0$ , 度為2的結點數為 $n_2$ , 則 $n_0=n_2+1$ 。

一棵深度為 $k$ , 且有 $2^k-1$ 個節點稱之為滿二元樹；深度為 $k$ ，有 $n$ 個節點的二元樹，若且唯若其每一個節點都與深度為 $k$ 的滿二元樹中，序號為 $1$ 至 $n$ 的節點對應時，稱之為完全二元樹。完全二元樹中重在節點標號對應。

Tree traversal 樹的遍歷

從二元樹的根節點出發，節點的遍歷分為三個主要步驟：對當前節點進行操作（稱為「訪問」節點，或者根節點）、遍歷左邊子節點、遍歷右邊子節點。訪問節點順序的不同也就形成了不同的遍歷方式。需要注意的是樹的遍歷通常使用遞迴的方法進行理解和實現，在訪問元素時也需要使用遞迴的思想去理解。

按照訪問根元素(當前元素)的前後順序，遍歷方式可劃分為如下幾種：

深度優先(depth-first)：先訪問子節點，再訪問父節點，最後訪問第二個子節點。根據根節點相對於左右子節點的訪問先後順序又可細分為以下三種方式。
1. 前序(pre-order)：先根後左再右
2. 中序(in-order)：先左後根再右
3. 後序(post-order)：先左後右再根
廣度優先(breadth-first)：先訪問根節點，沿著樹的寬度遍歷子節點，直到所有節點均被訪問為止，又稱為層次(level-order)遍歷。

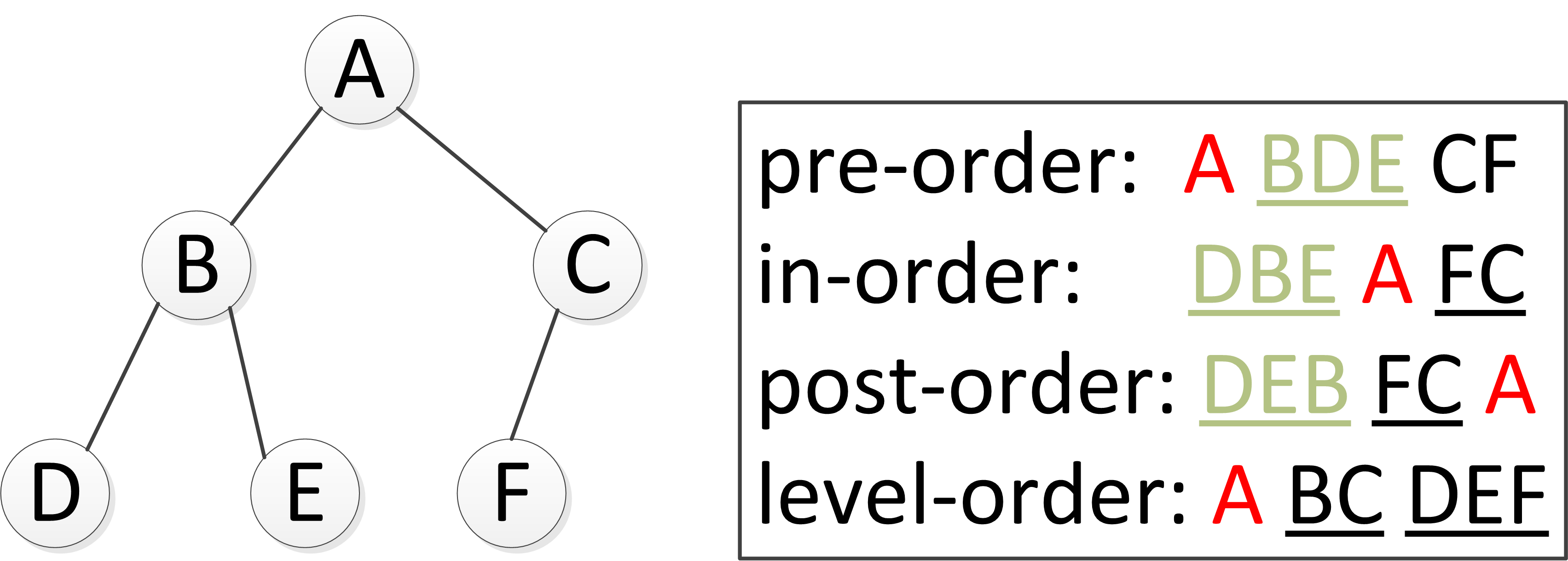
如下圖所示，遍歷順序在右側框中，紅色A為根節點。使用遞迴和整體的思想去分析遍歷順序較為清晰。

二元樹的廣度優先遍歷和樹的前序/中序/後序遍歷不太一樣，前/中/後序遍歷使用遞迴，也就是用堆疊(stack)的思想對二元樹進行遍歷，廣度優先一般使用隊列(queue)的思想對二元樹進行遍歷。

Binary Tree Traversal

節點定義

這裡的節點統一使用LeetCode的定義

Python

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None

C++

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

Java

public class TreeNode {
    public int val;
    public TreeNode left, right;
    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

樹類題的複雜度分析

對樹相關的題進行複雜度分析時可統計對每個節點被訪問的次數，進而求得總的時間複雜度。

leetcode

Binary Tree - 二元樹

Tree traversal 樹的遍歷

節點定義

Python

C++

Java

相關演算法——遞迴法遍歷

相關演算法——分治法(Divide & Conquer)

分治法思想

樹類題的複雜度分析