Linked List Cycle
Source
- leetcode: Linked List Cycle | LeetCode OJ
- lintcode: (102) Linked List Cycle
Given a linked list, determine if it has a cycle in it.
Example
Given -21->10->4->5, tail connects to node index 1, return true
Challenge
Follow up:
Can you solve it without using extra space?
題解 - 快慢指標
對於帶環鏈表的檢測,效率較高且易於實現的一種方式為使用快慢指標。快指標每次走兩步,慢指標每次走一步,如果快慢指標相遇(快慢指標所指內存為同一區域)則有環,否則快指標會一直走到NULL為止退出循環,返回false.
快指標走到NULL退出循環即可確定此鏈表一定無環這個很好理解。那麼帶環的鏈表快慢指標一定會相遇嗎?先來看看下圖。
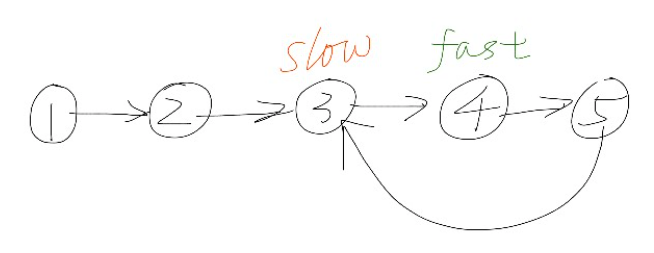
在有環的情況下,最終快慢指標一定都走在環內,加入第i次遍歷時快指標還需要k步才能追上慢指標,由於快指標比慢指標每次多走一步。那麼每遍歷一次快慢指標間的間距都會減少1,直至最終相遇。故快慢指標相遇一定能確定該鏈表有環。
C++
/**
* Definition of ListNode
* class ListNode {
* public:
* int val;
* ListNode *next;
* ListNode(int val) {
* this->val = val;
* this->next = NULL;
* }
* }
*/
class Solution {
public:
/**
* @param head: The first node of linked list.
* @return: True if it has a cycle, or false
*/
bool hasCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
while(fast and fast->next){
slow = slow -> next;
fast = fast -> next -> next;
if(slow == fast) return true;
}
return false;
}
};
源碼分析
- 異常處理,將
head->next也考慮在內有助於簡化後面的代碼。 - 慢指標初始化為
head, 快指標初始化為head的下一個節點,這是快慢指標初始化的一種方法,有時會簡化邊界處理,但有時會增加麻煩,比如該題的進階版。
複雜度分析
- 在無環時,快指標每次走兩步走到尾部節點,遍歷的時間複雜度為 .
- 有環時,最壞的時間複雜度近似為 . 最壞情況下鏈表的頭尾相接,此時快指標恰好在慢指標前一個節點,還需 n 次快慢指標相遇。最好情況和無環相同,尾節點出現環。
故總的時間複雜度可近似為 .