改进此页

Find Minimum in Rotated Sorted Array

Source

Problem

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

Find the minimum element.

Example

Given [4, 5, 6, 7, 0, 1, 2] return 0

Note

You may assume no duplicate exists in the array.

题解

如前节所述，对于旋转数组的分析可使用画图的方法，如下图所示，升序数组经旋转后可能为如下两种形式。

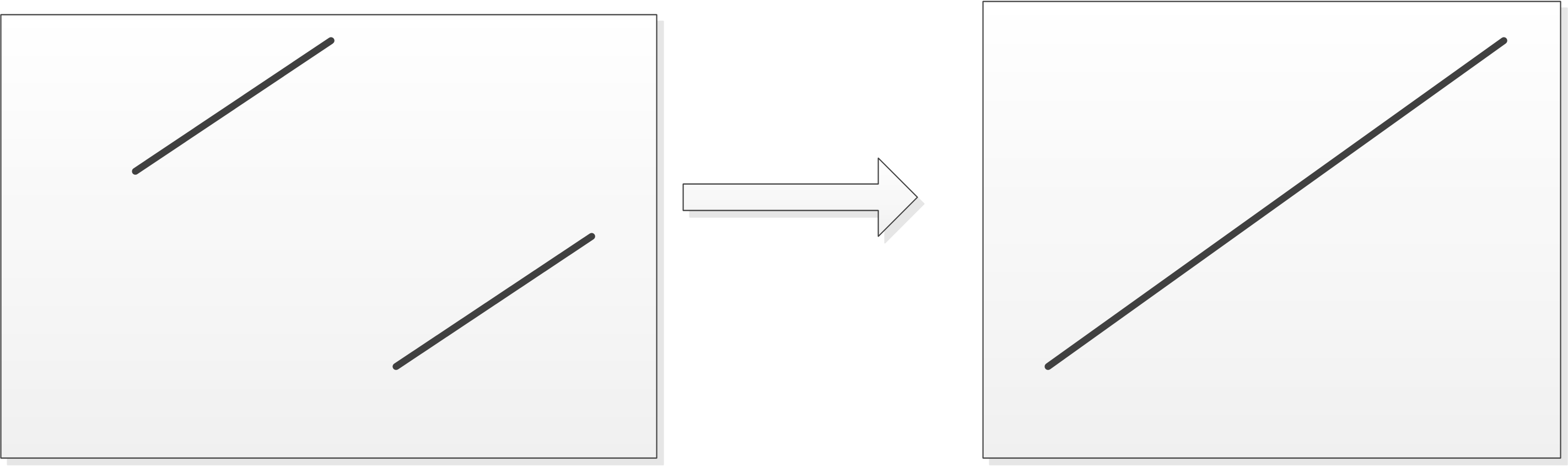
Rotated Array

最小值可能在上图中的两种位置出现，如果仍然使用数组首部元素作为target去比较，则需要考虑图中右侧情况。使用逆向思维分析，如果使用数组尾部元素分析，则无需图中右侧的特殊情况。不过考虑在内的话也算是一种优化。

C++

class Solution {
public:
    /**
     * @param num: a rotated sorted array
     * @return: the minimum number in the array
     */
    int findMin(vector<int> &num) {
        if (num.empty()) {
            return -1;
        }

        vector<int>::size_type start = 0;
        vector<int>::size_type end = num.size() - 1;
        vector<int>::size_type mid;
        while (start + 1 < end) {
            mid = start + (end - start) / 2;
            if (num[mid] < num[end]) {
                end = mid;
            } else {
                start = mid;
            }
        }

        if (num[start] < num[end]) {
            return num[start];
        } else {
            return num[end];
        }
    }
};

Java

public class Solution {
    /**
     * @param num: a rotated sorted array
     * @return: the minimum number in the array
     */
    public int findMin(int[] num) {
        if (num == null || num.length == 0) return Integer.MIN_VALUE;

        int lb = 0, ub = num.length - 1;
        // case1: num[0] < num[num.length - 1]
        // if (num[lb] < num[ub]) return num[lb];

        // case2: num[0] > num[num.length - 1] or num[0] < num[num.length - 1]
        while (lb + 1 < ub) {
            int mid = lb + (ub - lb) / 2;
            if (num[mid] < num[ub]) {
                ub = mid;
            } else {
                lb = mid;
            }
        }

        return Math.min(num[lb], num[ub]);
    }
}

源码分析

仅需注意使用num[end](使用 num[lb]不是那么直观)作为判断依据即可，由于题中已给无重复数组的条件，故无需处理num[mid] == num[end]特殊条件。

复杂度分析

由于无重复元素，平均情况下复杂度为 O(logn)O(\log n).