改进此页

Topological Sorting

Source

Given an directed graph, a topological order of the graph nodes is defined as follow:

For each directed edge A -> B in graph, A must before B in the order list.
The first node in the order can be any node in the graph with no nodes direct to it.
Find any topological order for the given graph.

Example For graph as follow:

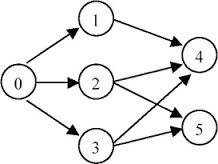
Topological Sorting

The topological order can be:

[0, 1, 2, 3, 4, 5]
[0, 2, 3, 1, 5, 4]
...
Note
You can assume that there is at least one topological order in the graph.

Challenge
Can you do it in both BFS and DFS?

题解1 - DFS and BFS

图搜索相关的问题较为常见的解法是用 DFS，这里结合 BFS 进行求解，分为三步走：

  1. 统计各定点的入度——只需统计节点在邻接列表中出现的次数即可知。
  2. 遍历图中各节点，找到入度为0的节点。
  3. 对入度为0的节点进行递归 DFS，将节点加入到最终返回结果中。

C++

/**
 * Definition for Directed graph.
 * struct DirectedGraphNode {
 *     int label;
 *     vector<DirectedGraphNode *> neighbors;
 *     DirectedGraphNode(int x) : label(x) {};
 * };
 */
class Solution {
public:
    /**
     * @param graph: A list of Directed graph node
     * @return: Any topological order for the given graph.
     */
    vector<DirectedGraphNode*> topSort(vector<DirectedGraphNode*> graph) {
        vector<DirectedGraphNode*> result;
        if (graph.size() == 0) return result;

        map<DirectedGraphNode*, int> indegree;
        // get indegree of all DirectedGraphNode
        indeg(graph, indegree);
        // dfs recursively
        for (int i = 0; i < graph.size(); ++i) {
            if (indegree[graph[i]] == 0) {
                dfs(indegree, graph[i], result);
            }
        }

        return result;
    }

private:
    /** get indegree of all DirectedGraphNode
     *
     */
    void indeg(vector<DirectedGraphNode*> &graph,
                  map<DirectedGraphNode*, int> &indegree) {

        for (int i = 0; i < graph.size(); ++i) {
            for (int j = 0; j < graph[i]->neighbors.size(); j++) {
                if (indegree.find(graph[i]->neighbors[j]) == indegree.end()) {
                    indegree[graph[i]->neighbors[j]] = 1;
                } else {
                    indegree[graph[i]->neighbors[j]] += 1;
                }
            }
        }
    }

    void dfs(map<DirectedGraphNode*, int> &indegree, DirectedGraphNode *i,
             vector<DirectedGraphNode*> &ret) {

        ret.push_back(i);
        indegree[i]--;
        for (int j = 0; j < i->neighbors.size(); ++j) {
            indegree[i->neighbors[j]]--;
            if (indegree[i->neighbors[j]] == 0) {
                dfs(indegree, i->neighbors[j], ret);
            }
        }
    }
};

源码分析

C++中使用 unordered_map 可获得更高的性能，私有方法中使用引用传值。

复杂度分析

以 V 表示顶点数，E 表示有向图中边的条数。

首先获得节点的入度数，时间复杂度为 O(V+E)O(V+E), 使用了哈希表存储，空间复杂度为 O(V)O(V). 遍历图求得入度为0的节点，时间复杂度为 O(V)O(V). 仅在入度为0时调用 DFS，故时间复杂度为 O(V+E)O(V+E).

需要注意的是这里的 DFS 不是纯 DFS，使用了 BFS 的思想进行了优化，否则一个节点将被遍历多次，时间复杂度可能恶化为指数级别。

综上，时间复杂度近似为 O(V+E)O(V+E), 空间复杂度为 O(V)O(V).

题解2 - BFS

拓扑排序除了可用 DFS 求解外，也可使用 BFS, 具体方法为：

  1. 获得图中各节点的入度。
  2. BFS 首先遍历求得入度数为0的节点，入队，便于下一次 BFS。
  3. 队列不为空时，弹出队顶元素并对其邻接节点进行 BFS，将入度为0的节点加入到最终结果和队列中，重复此过程直至队列为空。

C++

/**
 * Definition for Directed graph.
 * struct DirectedGraphNode {
 *     int label;
 *     vector<DirectedGraphNode *> neighbors;
 *     DirectedGraphNode(int x) : label(x) {};
 * };
 */
class Solution {
public:
    /**
     * @param graph: A list of Directed graph node
     * @return: Any topological order for the given graph.
     */
    vector<DirectedGraphNode*> topSort(vector<DirectedGraphNode*> graph) {
        vector<DirectedGraphNode*> result;
        if (graph.size() == 0) return result;

        map<DirectedGraphNode*, int> indegree;
        // get indegree of all DirectedGraphNode
        indeg(graph, indegree);
        queue<DirectedGraphNode*> q;
        // bfs
        bfs(graph, indegree, q, result);

        return result;
    }

private:
    /** get indegree of all DirectedGraphNode
     * 
     */
    void indeg(vector<DirectedGraphNode*> &graph, 
                  map<DirectedGraphNode*, int> &indegree) {

        for (int i = 0; i < graph.size(); ++i) {
            for (int j = 0; j < graph[i]->neighbors.size(); j++) {
                if (indegree.find(graph[i]->neighbors[j]) == indegree.end()) {
                    indegree[graph[i]->neighbors[j]] = 1;
                } else {
                    indegree[graph[i]->neighbors[j]] += 1;
                }
            }
        }
    }

    void bfs(vector<DirectedGraphNode*> &graph, map<DirectedGraphNode*, int> &indegree,
             queue<DirectedGraphNode *> &q, vector<DirectedGraphNode*> &ret) {

        for (int i = 0; i < graph.size(); ++i) {
            if (indegree[graph[i]] == 0) {
                ret.push_back(graph[i]);
                q.push(graph[i]);
            }
        }

        while (!q.empty()) {
            DirectedGraphNode *cur = q.front();
            q.pop();
            for(int j = 0; j < cur->neighbors.size(); ++j) {
                indegree[cur->neighbors[j]]--;
                if (indegree[cur->neighbors[j]] == 0) {
                    ret.push_back(cur->neighbors[j]);
                    q.push(cur->neighbors[j]);
                }
            }
        }
    }
};

源码分析

C++中在判断入度是否为0时将对 map 产生副作用，在求入度数时只有入度数大于等于1才会出现在 map 中，故不在 map 中时直接调用 indegree 方法将产生新的键值对，初始值为0，恰好满足此题需求。

复杂度分析

同题解1 的分析，时间复杂度为 O(V+E)O(V+E), 空间复杂度为 O(V)O(V).

Reference